Again: not happy about this post. It seems like I’m terrible at explaining my thoughts on paper. Well, it’s not as if I didn’t know that, but it’s worse than I thought. Anyway, solving two problems of Erdos and Graham in 24 hours is not something I’m not going to blog about;
In their book, Erdös and Graham also ask the following, I think more general, question:
Let 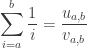 . For fixed
. For fixed  what is the least
what is the least 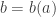 such that
such that  ? In fact, is there always such a
? In fact, is there always such a  for every
for every  ? Using the result of the previous post, I am able to show that
? Using the result of the previous post, I am able to show that  exists for every
exists for every  , and, even more,
, and, even more,  for all
for all  . In a very strict sense this is best possible, as
. In a very strict sense this is best possible, as  . I will use the notation from the previous two posts, along with the new definition:
. I will use the notation from the previous two posts, along with the new definition: 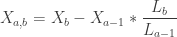 . We now have:
. We now have:
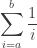

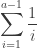
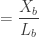

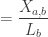
With 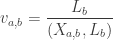 . Now, let
. Now, let  be such that
be such that 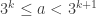 . Let
. Let  . Note that
. Note that 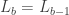 in that case. So we’re done if we can show
in that case. So we’re done if we can show  . And the proof of this is not very hard using the result of the previous post;
. And the proof of this is not very hard using the result of the previous post;
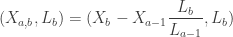

Now, the only difference with 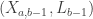 is the term
is the term  . This term doesn’t affect anything, except for possibly factors of
. This term doesn’t affect anything, except for possibly factors of  and
and 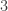 (since
(since 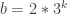 ). But we already know that
). But we already know that 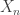 is odd for all
is odd for all  , which implies
, which implies 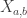 is also odd for all
is also odd for all  with
with 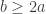 . So the only thing that the term
. So the only thing that the term  might change, is the divisibility of
might change, is the divisibility of 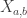 by
by 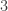 . And, indeed, we showed in the previous two posts that
. And, indeed, we showed in the previous two posts that  for
for 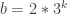 , while
, while 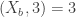 . So, since
. So, since  by our choice of
by our choice of  ,
, 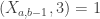 , while
, while 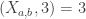 . In other words:
. In other words:  , and this finishes our proof.
, and this finishes our proof.
To recapture: Let  be fixed. Let
be fixed. Let  be such that
be such that 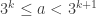 . Choose
. Choose  . Then:
. Then: 
infinitely often, can be quite easily generalised and yield a lot more that way. And it also gives some insight in why it’s hard to show
infinitely often; maybe it’s not true! The theorem I will prove later (either today or tomorrow) will be:
be a given natural number and
be a given prime. Let
be the unique number smaller than
such that
for some
. Then the following two are equivalent:
, with
the least common multiple of